Key Exchange, TLS1.2 and TLS1.3

By / / 开发 / Leave a Comment

Above all, we need to know that asymmetric encryption is much slower than symmetric encryption. So, in practice, we usually use them in combination. First, asymmetric encryption is used to exchange a shared key, which is symmetrically encrypted; then, in the subsequent communication, the shared key is used to symmetrically encrypt all messages.

首先，我们需要知道，非对称加密比对称加密要慢的多。所以在实际应用中，通常将二者结合起来使用。先使用非对称加密来交换一个共享密钥，该密钥是对称加密的；然后在后续会话中，使用该共享密钥对数据进行对称加密。

Key Exchange

Key Exchange, in cryptography, refers to the protocol by which two communicating parties exchange a cryptographic key on an open channel. Of course, the key exchange usually does not transmit keys directly on the open channel but rather exchanges certain factors for calculating the key(DH key exchange) or exchanges the key encrypted by a public key(RSA key exchange). Then, both parties will calculate the same key (aka. shared key or shared secret) for the following data encryption transmission.

Common key exchange protocols include RSA, DH, and ECDH.

Key Exchange 密钥交换，在密码学中是指通信双方在公开信道上交换密钥的方式。当然，密钥交换并不是说在公开信道上直接传输密钥，而是交换计算密钥的某些因子(DH 密钥交换)，或者是用公钥加密过的密钥(RSA 密钥交换)，然后双方再各自计算出这个密钥(通常被叫做共享密钥)，用来做后续的数据加密传输。

常见的密钥交换协议有 RSA, DH, ECDH。

RSA Key Exchange

RSA is an asymmetric encryption algorithm, and its basic principle can be simplified as follows. The selection of the three numbers E, D, and N must meet certain mathematical requirements, which will not be discussed in depth here.

Ciphertext = Plaintextᴱ mod N  // RSA encryption, Pubic key={E, N}
Plaintext = Ciphertextᴰ mod N  // RSA decryption, Private key={D, N} (结城浩, 2016)

Here is a simple example:

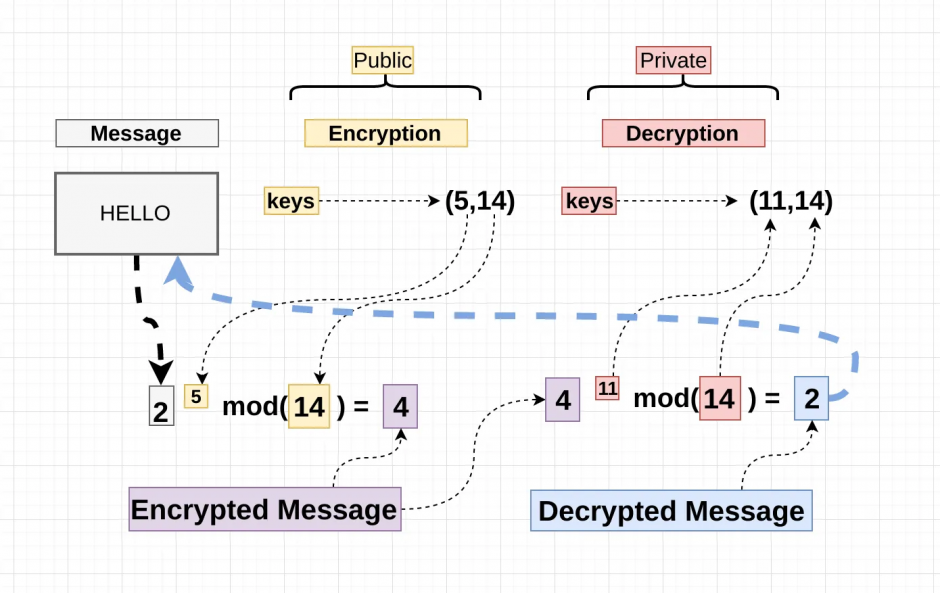
source: https://medium.com/hackernoon/how-does-rsa-work-f44918df914b

If RSA is used in the key exchange process, the general steps are as follows:

  1. Bob sends the public key to Alice;
  2. Alice generates a shared symmetric key, encrypts it, and then sends it to Bob;
  3. Bob uses his private key to decrypt the shared key;
  4. Shared key exchange completed.

RSA 是一种非对称加密算法，它的基本原理可以简化成如下形式。其中 E, D, N 三个数字的选择需要满足一定数学条件，这里不做深入讨论。

密文 = 明文ᴱ mod N    // RSA 加密, 公钥={E, N}
明文 = 密文ᴰ mod N    // RSA 解密, 私钥={D, N} (结城浩, 2016)

这里有一个简单的例子：见上图。

如果将 RSA 用在密钥交换过程中，就是

  1. Bob 将其公钥发送给 Alice；
  2. Alice 计算出一个共享密钥后，使用 Bob 的公钥加密再发送给 Bob；
  3. Bob 私用私钥解密后获得共享密钥；
  4. 密钥交换完成。

Diffie-Hellman(DH) Key Exchange

DH key exchange was the first published public-key algorithm(asymmetric encryption) and was widely used in key exchange.

DH key exchange steps are as follows:

  1. Agree on public parameters
    The two parties (let’s call them Alice and Bob) choose a large prime number p and a base g (an integer less than p, and g is a primitive root modulo p) and share them publicly;
  2. Each party generates private keys
    • Alice randomly chooses a private key a (1 < a < p);
    • Bob also chooses a private key b randomly (1 < b < p).
  3. Calculate public keys and Exchange public keys
    • Alice calculates the public key A = gᵃ mod p;
    • Bob calculates the public key B = gᵇ mod p
    • Alice and Bob send their public keys(A, B) to each other. This exchange can be done over an insecure channel.
  4. Each party computes the shared key
    Alice calculates the shared key s = Bᵃ mod p;
    Bob calculates the shared key s = Aᵇ mod p;
    Due to the properties of mathematics, the s Alice and Bob calculated the same.
  5. Sending messages encrypted by the shared key
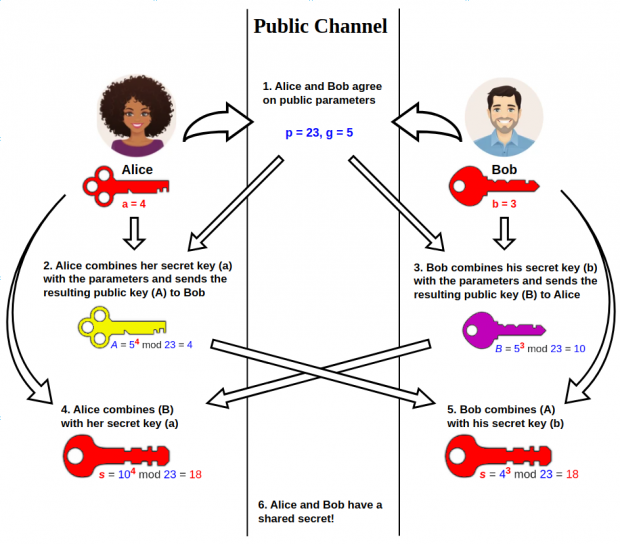
source: https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange#/media/File:DiffieHellman.png

DH 密钥交换步骤：

  1. 选择公开参数
    通信双方(通常称为 Alice 和 Bob)选择一个大型素数 p 和一个生成元 g (通常是小于 p 的整数，并且 g 是 p 的原根 primitive root, 即 gⁱ mod p 可以生成所有 [1, p) 之间的的整数)，并将这两个数公开；
  2. 生成私有密钥
    • Alice 随机选择一个私钥 a (1 < a < p).
    • Bob 随机选择一个私钥 b (1 < b < p).
  3. 计算公钥并交换
    • Alice 计算公钥 A = gᵃ mod p.
    • Bob 计算公钥 B = gᵇ mod p.
    • 双方公开交换公钥(A, B)，这个交换可以在不安全的通道上进行。
  4. 计算共享密钥
    • Alice 计算共享密钥 s = Bᵃ mod p；
    • Bob 计算共享密钥 s = Aᵇ mod p；
    • 由于数学的性质，Alice 和 Bob 计算出的 s 是相同的。
  5. 使用该共享密钥进行消息加密与解密

Elliptic-curve Diffie–Hellman(ECDH) Key Exchange

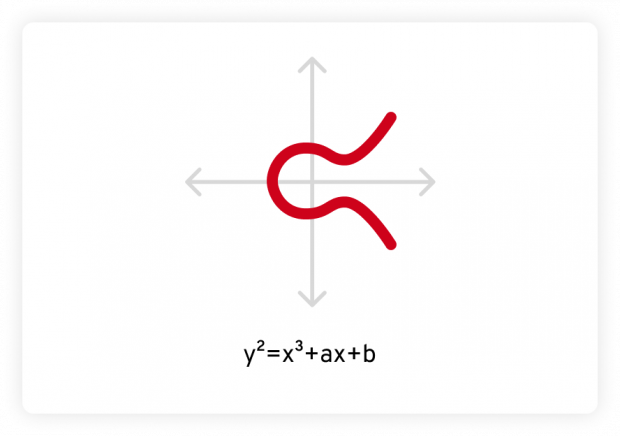
Elliptic-curve Diffie–Hellman (ECDH) is a variant of the Diffie–Hellman protocol using elliptic-curve cryptography. It has better computing performance and security than the classical DH algorithm that uses modular arithmetic. The elliptic curve is a curve described by the equation y2 = x3 + ax + b, and its plot is as follows:

source: https://www.keepersecurity.com/blog/2023/06/07/what-is-elliptic-curve-cryptography/

ECDH key exchange steps are similar to the classical DH algorithm, but the calculation method is different:

  1. Agree on public parameters
    Both parties (Alice and Bob) agree on the following elliptic curve parameters:
    • Elliptic Curve function EC,
    • Generator point G,
  2. Generate private keys and public keys
    • Private keys: Each party generates a private key. Alice gets a , and Bob gets b. These private keys are kept secret and never shared.
    • Public keys: Each party computes their corresponding public key by performing elliptic curve point multiplication with the generator point. Alice gets Pa = G•a, and Bob gets Pb = G•b.
    • The multiplication operation • here is the scalar multiplication of the elliptic curve, not the ordinary multiplication.
  3. Exchange public keys
    Alice and Bob send their public keys to each other. This exchange can be done over an insecure channel.
  4. Each party computes the shared key
    • Alice: K = a•Pb = a•(b•G)
    • Bob: K = b•Pa = b•(a•G)
    • According to the elliptic curve multiplication, the K calculated by both parties is consistent.
  5. Sending messages encrypted by the shared key

ECDH 是采用 椭圆曲线密码 的 DH 算法，比起使用模运算的传统 DH 算法，它有更好的计算性能与安全性。椭圆曲线是由方程 y2 = x3 + ax + b 描述的曲线，其绘制图形如下：

ECDH 密钥交换步骤, 跟传统 DH 的逻辑一样，只是计算方法不同:

  1. 选择公开参数
    双方选择一个椭圆曲线 EC 和基点 G.
  2. 各自生成私钥和公钥
    • 私钥: 每方生成一个随机私钥(一个大整数), Alice 的私钥为 a, Bob 的私钥为 b.
    • 公钥: 通过基点 G 和私钥生成公钥, Alice 的公钥 Pa = G•a, Bob 的公钥为 Pb = G•b.
    • 这里的点乘运算 • 是椭圆曲线的标量乘法，不是普通的乘法.
  3. 交换公钥
    双方公开交换公钥，这个交换可以在不安全的通道上进行。
  4. 计算共享密钥
    • Alice: K = a•Pb = a•(b•G)
    • Bob: K = b•Pa = b•(a•G)
    • 根据椭圆曲线的特性，双方计算出来的 K 是一致的。
  5. 使用该共享密钥进行消息加密

Forward secrecy

RSA, as well as basic DH and ECDH, lack forward security. For DH and ECDH, we can choose to reselect a private key for each session, which can ensure forward security. This is called DHE and ECDHE. E here stands for Ephemeral, which means the private key is temporary and only used in one session.

Forward secrecy, 前向安全性。 RSA, 以及基本的 DH, ECDH 都缺乏前向安全性。对于 DH, ECDH 可以在每次会话时都重新选择私钥，重新计算共享密钥，这样就能保证前向安全，这就叫做 DHE, ECDHE。E 即 Ephemeral, 表示这个私钥是临时的。

Preventing MITM attacks

From the basic steps of key exchange mentioned above, we can see that they are all vulnerable to man-in-the-middle attacks, so in practical applications, certificate verification steps need to be added. I will show this in the TLS handshake following.

从上述密钥交换的基本步骤中，可以看出它们都容易被中间人攻击，所以在实际应用中，需要加上证书验证的步骤。这点我们可以在后面的 TLS 握手中看到。

TLS

TLS（Transport Layer Security) is the successor to SSL (Secure Sockets Layer), which has been largely deprecated since 1999, and even though the name SSL is used, it is actually TLS.

TLS only uses asymmetric encryption during the handshake phase and then uses a key exchange algorithm to negotiate a set of symmetric keys (called shared keys or session keys). It is these symmetric keys that are used in the data transfer phase (because they are more computationally efficient than asymmetric encryption).

TLS（Transport Layer Security，传输层安全协议）和 SSL（Secure Sockets Layer，安全套接字层协议）之间的关系是：TLS 是 SSL 的后继版本。SSL 在1999年后基本已经不再使用了，即使用到了 SSL 这个名称，其实内里也是 TLS。

TLS 只有在握手阶段是使用非对称加密，然后使用密钥交换算法协商出一组对称密钥(叫做 shared keys 或者 session keys)。在数据传输阶段使用的就是这组对称密钥（因为计算效率比非对称加密高）。

TLS Session vs. TLS Connection

  • TLS Session
    • Shared among multiple TLS connections, a session can have multiple connections (a connection can only correspond to one session). This is to support efficient session reuse without needing a new handshake for each connection.
    • Contains a set of cryptographic parameters (especially the master secret).
    • The life cycle is longer than the connection’s, and a session resumption mechanism exists.
  • TLS Connection
    • One connection is associated with one session. (One session can be associated with multiple connections).
    • It contains session keys used for data transmission (session keys actually include Initialization Vectors, symmetric encryption keys, and MAC secrets).
    • The life cycle is shorter and limited to one data transmission.
    • It can be understood that each HTTPS request corresponds to a connection (without using connection reuse).

Pre-master secret, Master secret, and Session keys (预主密钥，主密钥与会话密钥)

FeaturesPre-Master Secret (预主密钥)Master Secret (主密钥)Session Keys (会话密钥)
Generation 生成阶段Generated by the key exchange algorithm during the handshake phase
在握手阶段由密钥交换算法生成		Derived from the pre-master secret key via a Pseudo-Random Function during the handshake phase
在握手阶段通过伪随机数生成函数从预主密钥派生		After the handshake is completed, multiple session keys are derived from the master key
握手完成后，通过主密钥进一步派生出多个密钥
Purpose 用途To generate the master key
用于生成主密钥		To generate the session keys
用于生成会话密钥		For actual data encryption, authentication, and message integrity
用于实际的数据加密、认证和消息完整性
Participant 参与者The client and server negotiate to generate
客户端和服务器协商生成		The client and server each calculate the same master key
客户端和服务器各自计算相同的主密钥		The client and server use the same session keys
客户端和服务器各自使用相同的会话密钥
Lifetime 存续时间Only exists during the handshake, short-lived
仅在握手期间存在，短暂		Valid throughout the session
整个会话期间有效		Valid for specific encryption/authentication operations and may be rotated
具体加密/认证操作期间有效，可能会轮换
Directly used for communication 是否直接用来通信NoNoYes

TLS1.2 handshake

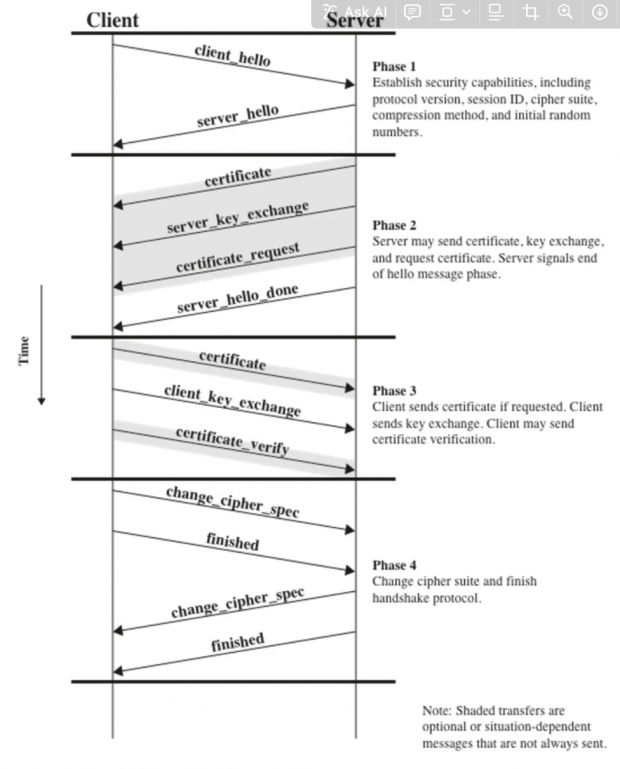
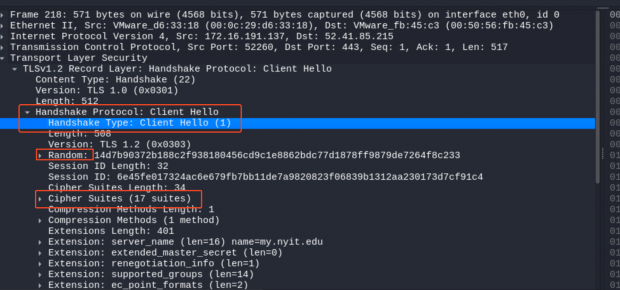
Step 1: ClientHello

  • Client 发送 ClientHello 消息给服务器，包含：
    • 客户端支持的 TLS 版本（如 TLS 1.2）。
    • 客户端支持的加密套件列表（如 AES、RSA、ECDHE 等）。
    • 一个随机数（Client Random）用于后续密钥生成。
    • 支持的压缩方法和其他扩展选项。
    • say hello 阶段不加密
Client Hello Package (captured by Wireshark)

Step 2: ServerHello

  • 服务器响应 ServerHello 消息，包含：
    • 服务器选择的 TLS 版本（例如 TLS 1.2）。
    • 选择的加密套件（根据客户端提供的选项）。
    • 另一个随机数（Server Random），用于密钥生成。
    • 服务器的数字证书，用于身份验证，证书中包含服务器的公钥。(certificate + pubkey + signature)
    • say hello 阶段不加密

如果服务器要求客户端认证（如双向 TLS），它还会请求客户端的证书(certificate_request 包)。

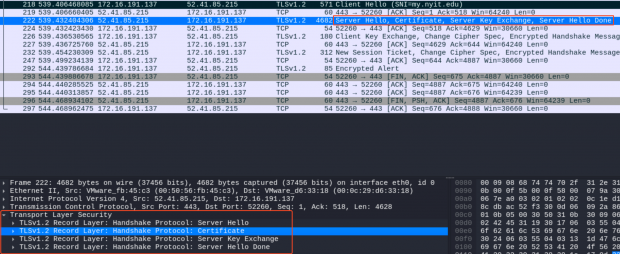
Server Hello Package (captured by Wireshark)

Step 3: Verification and Key Exchange

  • 客户端验证服务器证书 (certificate_verify 包)
  • 生成 预主密钥（Pre-Master Secret）(发送 client_key_exchange 包)
    • 如果使用的是 RSA 密钥交换，客户端独立生成预主密钥后使用服务器公钥加密并发送给服务器。
    • 如果使用的是 Diffie-Hellman 密钥交换，则双方交换 DH 参数，然后各自计算出相同的预主密钥。
  • 双方根据 Client Random、Server Random 和预主密钥生成主密钥(Master secret)，以及生成 session keys 用于对数据传输进行加密。
  • 所有密钥都计算完后，发送 change_cipher_spec 包
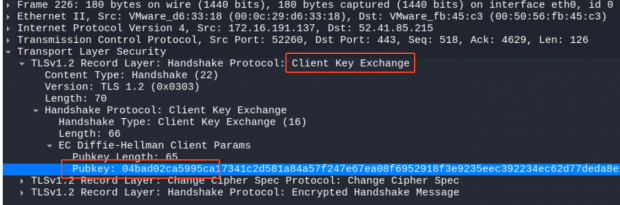
Client Key Exchange Package (captured by Wireshark)

Step 4: Handshake finished and start encrypted communication

  • 客户端和服务器随后通过 Finished 消息向对方确认握手过程是否成功。双方会使用生成的会话密钥(session keys)来加密这条 Finished 消息。
  • 握手完成后，客户端和服务器使用协商出的对称密钥开始加密通信

TLS1.3 handshake

  • TLS 1.3 在发送 hello 包的时候就已经包含了密钥交换的一些安全参数，从而减少握手的步骤。
  • TLS 1.3 不再支持 RSA 密钥交换方式，只支持 DH 系的密钥交换(DH 或者 ECDHE)。
  • TLS 1.3 握手只需要 1 个 RTT(Round trip time, 一来一回)， TLS 1.2 握手需要 2 个 RTT。

Step 1: Client Hello + Client Cryptographic Parameters

  • 客户端发送 Client Hello 包，其中包含:
    • 客户端随机数（ClientHello.random）
    • 支持的加密套件（Cipher suites）
    • 支持的密钥交换算法，以及所需的安全参数(包括 client key_share, 可以简单理解为就是 DH 方法的公钥)

Step 2: Server Hello + Server Cryptographic Parameters

  • 服务器回应 Server Hello 包，其中包含:
    • 服务器随机数
    • 服务器选中的加密套件 (Cipher suites)
    • 服务器的 key_share (服务器的 DH 公钥)

Step 3: Both parties calculate shared keys and begin the encrypted transmission

  • 服务器计算出共享密钥，发送 change cipher spec 包，然后就开始使用共享密钥加密并发送消息(Finished)。 （我理解是 TLS 1.3 这里的共享密钥包括了，类似 TLS 1.2 中的 预主密钥，session keys 的所有密钥，当然可能不再叫这些名字了。）
  • 客户端计算出共享密钥，发送 change cipher spec 包，然后就开始使用共享密钥加密并发送消息。

Cipher suite naming scheme (加密套件的命名规则)

Each cipher suite has a unique name used to identify it and describe its algorithmic contents. The naming of cipher suites usually follows certain rules and usually consists of the following segments, separated by underscores:

[protocol]_[key exchange algorithm]_[authentication algorithm]_[session encryption algorithm]_[message authentication algorithm]

Take TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256 for example.

  • TLS
    Defines the protocol this cipher suite is for; it will usually be TLS.
  • ECDHE
    Indicates the key exchange algorithm being used.
  • RSA
    Authentication mechanism during the handshake. To authenticate the other party is who he claims to be.
  • AES_128_GCM
    Session cipher algorithm. After the handshake, the session communication between the two parties will be encrypted using a symmetric encryption algorithm.
  • SHA256
    Indicates the message authentication algorithm used to generate a MAC(Message Authentication Code) and authenticate a message.

References

  1. Wikipedia contributors. (2024a, May 5). Key exchange. Wikipedia. https://en.wikipedia.org/wiki/Key_exchange
  2. Wikipedia contributors. (2024b, September 5). Cipher suite. Wikipedia. https://en.wikipedia.org/wiki/Cipher_suite
  3. Wikipedia contributors. (2024c, October 12). Diffie–Hellman key exchange. Wikipedia. https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange
  4. Wikipedia contributors. (2024d, October 14). Elliptic-Curve Diffie–Hellman. Wikipedia. https://en.wikipedia.org/wiki/Elliptic-curve_Diffie%E2%80%93Hellman
  5. 结城浩. (2016). 图解密码技术: 第3版.

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top